glosario de simbolos:
ÁNGULO ..................................... ∢
ANGULO RECTO ............................ ∡
APROXIMADAMENTE IGUAL .......... ≐, ≈
ARCO DE A a B ............................... A⁀B
CARDINAL EL CONJUNTO X, Y...... |{ X, Y}|
CÍRCULO ....................................... ⊙
CONGRUENTE CON .......................... ≌
CONJUNTO A ................................. A
CONJUNTO TOMADO POR LOS
ELEMENTOS: a, b y c.......................... A = {a, b, c}
CONJUNTO DE LOS NÚMEROS
ENTEROS ....................................... Z
CONJUNTO DE LOS NÚMEROS
NATURALES ................................... N
CONJUNTO DE LOS NÚMEROS
RACIONALES ................................ Q
CONJUNCIÓN ........................................… L
CONJUNTO VACÍO ........................ { }, Ø
DEFINIDO IGUAL ........................... : =
DISTINTO, NO IGUAL .................... ≠
DIVIDIDO ENTRE .......................... :
ES ELEMENTO DE ........................ є
ES SUBCONJUNTO DE ................. ⊂
EQUIVALENCIA .......................... ↔
FUNCIÓN f ........................................… f
IDENTIFICACIÓN IGUAL ................... ≡
IGUAL ........................................… =
IMPLICACIÓN ...................................... ⇒
INFINITO ........................................… ∞
INTERSECTADO ......................... ∩
MÁS ........................................… +
MÁS O MENOS ................................... ±
MAYOR QUE ....................................... >
MAYOR IGUAL QUE .......................... ≥
MEDIDA DE SEGMENTO AB ........ | AB |
MENOR QUE ........................................ <
MENOR IGUAL QUE ........................... ≤
MENOS ........................................… -
MUY GRANDE RESPECTO A .......... >>
MUY PEQUEÑO RESPECTO A ....... <<
NO ........................................… ┒
NO ES ELEMENTO DE ..................... ∉
NO ES SUBCONJUNTO DE ............ ⊄
NO ES CIERTA LA PROPOSICIÓN .. ∼p
O (LA DISYUNCIÓN) ............................ V
PAR ORDENADO a, b ........................... (a, b)
PARALELA ........................................… ∥
PI....................................…
POR ........................................… Ï
POR CIENTO ...................................... %
POR TANTO, POR CONSIGUIENTE .. \
PRODUCTO CARTESIANO DE LOS
ELEMENTOS M, N ................................... MÏN
RAYA DE FRACCIÓN ............................ / , ¾
RECTA r ........................................… r
RECTA QUE PASA POR LOS
PUNTO A, B ........................................… AB
SE CORRESPONDE CON .................... ≙
SEGMENTO ENTRE LOS PUNTOS A, B .. AB
TAL QUE ........................................… /
TRIANGULO ........................................ ∆
UNIDO CON ........................................… ∪
Lugar Espacial de Calculo Diferencial
martes, 5 de junio de 2012
1.- Precalculo
1.1 Sistema de coordenadas lineales y rectangulares
Coordenadas lineales
Un
punto cualquiera de una recta puede asociarse y representarse con un número
real, positivo si está situado a la derecha de un punto O, y negativo si
está a la izquierda. Dicho punto se llama origen de coordenadas O (letra
O) y se asocia al valor 0 (cero).
Corresponde
a la dimensión uno, que se representa con el eje X, en el cual se define un
origen de coordenadas, simbolizado con la letra O (O de origen) y
un vector unitario en la dirección positiva de las x: I.
Este
sistema de coordenadas es un espacio vectorial de dimensión uno, y se le pueden
aplicar todas las operaciones correspondientes a espacios vectoriales. También
se le llama recta real.
Un punto:
coordenadas rectangulares
Se
llama sistema de coordenadas rectangulares al formado por dos rectas
perpendiculares entre si que se cortan en el punto O, llamado origen del
sistema. A la recta horizontal se le llama eje X o de las abscisas y a la recta
vertical eje Y o de las ordenadas.
Determinan
cuatro regiones, denominadas cuadrantes, numerados siguiendo un sentido
contrario a las agujas del reloj. La dirección positiva del eje X es hacia la
derecha y la del eje Y es hacia arriba.
Para
cualquier punto P en el plano determinado por estas rectas existen dos números
reales llamados coordenadas de P. La coordenada x sobre el eje X viene dada por
la longitud del segmento OA, mientras la coordenada y sobre el eje Y
viene dada por la longitud del segmento OB. Véase la figura. Esto se
representa por P(x, y).
(-4,2), (-5,-6), (3, 2).
ejercicios:
localiza los siguientes puntos en la recta real:
13/5, 12/3, 36/7, -13/5, -12/3, -36/7, 0/11.
localiza los siguientes puntos en el plano cartesiano:
(-6.3, 5), (5.3, 2), ( -7,2.5).
1.2
desigualdades
En
matemáticas, una desigualdad es una relación que se da entre dos valores
cuando estos son distintos (en caso de ser iguales, lo que se tiene es una
igualdad).
Si los
valores en cuestión son elementos de un conjunto ordenado, como los enteros o
los reales, entonces pueden ser comparados.
- La notación a < b significa a es menor que b;
- La notación a > b significa a es mayor que b;
estas
relaciones se conocen como desigualdades estrictas, puesto que a
no puede ser igual a b; también puede leerse como "estrictamente
menor que" o "estrictamente mayor que".
- La notación a ≤ b significa a es menor o igual que b;
- La notación a ≥ b significa a es mayor o igual que b;
estos tipos
de desigualdades reciben el nombre de desigualdades amplias (o no
estrictas).
- La notación a ≪ b significa a es mucho menor que b;
- La notación a ≫ b significa a es mucho mayor que b;
esta
relación indica por lo general una diferencia de varios órdenes de magnitud.
- La notación a ≠ b significa que a no es igual a b. Tal expresión no indica si uno es mayor que el otro, o siquiera si son comparables.
.
Ejemplos:
ejercicios:
1) 4 + 9x > –2 + 7x2) 5 – 3x < 13 + 3x

Propiedades
Las desigualdades están gobernadas por las
siguientes propiedades. Notar que, para las propiedades transitividad, adición,
sustracción, multiplicación y división, la propiedad también se mantiene si los
símbolos de desigualdad estricta (< y >) son reemplazados por sus
correspondientes símbolos de desigualdad no estricta (≤ y ≥).
Transitividad
- Para números reales arbitrarios a,b y c:
·
Si a > b y b > c entonces a
> c.
·
Si a < b y b < c entonces a
< c.
·
Si a > b y b = c entonces a
> c.
·
Si a < b y b = c entonces a
< c.
Adición y sustracción
- Para números reales arbitrarios a,b y c:
·
Si a < b entonces a + c < b + c
y a − c < b − c.
·
Si a > b entonces a + c > b + c
y a − c > b − c.
Multiplicación y división
- Para números reales arbitrarios a y b, y c diferente de cero:
·
Si c es positivo y a < b entonces ac
< bc y a/c < b/c.
·
Si c es negativo y a < b entonces ac
> bc y a/c > b/c.
Opuesto
- Para números reales arbitrarios a y b:
·
Si a < b entonces −a > −b.
·
Si a > b entonces −a < −b.
Recíproco
- Para números reales a y b distintos de cero, ambos positivos o negativos a la vez:
·
Si a < b entonces 1/a > 1/b.
·
Si a > b entonces 1/a < 1/b.
- Si a y b son de distinto signo:
·
Si a < b entonces 1/a < 1/b.
·
Si a > b entonces 1/a > 1/b.
Definición de intervalo
Se
llama intervalo al conjunto de números reales comprendidos entre
otros dos dados: a y b que se llaman extremos del intervalo.
Intervalo abierto
Intervalo
abierto, (a, b),
es el conjunto de todos los números reales mayores que a y menores que b.
(a,
b) = {x 
 / a < x < b}
/ a < x < b}
Intervalo cerrado
Intervalo
cerrado, [a, b],
es el conjunto de todos los números reales mayores o iguales que a y menores
o iguales que b.
[a,
b] = {x 
 / a ≤ x ≤ b}
/ a ≤ x ≤ b}
Intervalo semiabierto por la izquierda
Intervalo
semiabierto por la izquierda,
(a, b], es el conjunto de todos los números reales mayores que a y
menores o iguales que b.
(a,
b] = {x 
 / a < x ≤ b}
/ a < x ≤ b}
Intervalo semiabierto por la derecha
Intervalo
semiabierto por la derecha,
[a, b), es el conjunto de todos los números reales mayores o iguales
que a y menores que b.
[a,
b) = {x 
 / a ≤ x < b}
/ a ≤ x < b}
ejercicios:
Expresa en lenguaje matemático los siguientes intervalos:

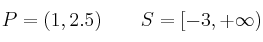

![Q=[-2,3] \qquad T=(2, +\infty) Q=[-2,3] \qquad T=(2, +\infty)](http://matematicasies.com/local/cache-TeX/f00c8e4b00cd34418276d7a56a52f38b.png)

![R=[-7,0] \qquad I=(-5, 2] R=[-7,0] \qquad I=(-5, 2]](http://matematicasies.com/local/cache-TeX/b088ec574587b57d7f8d50c5ade01859.png)
Representa gráficamente y expresa simbólicamente las siguientes expresiones:

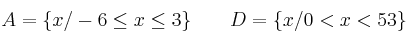

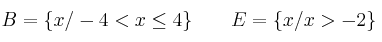

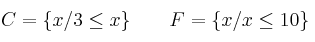
Suscribirse a:
Comentarios (Atom)


