Definición de intervalo
Se
llama intervalo al conjunto de números reales comprendidos entre
otros dos dados: a y b que se llaman extremos del intervalo.
Intervalo abierto
Intervalo
abierto, (a, b),
es el conjunto de todos los números reales mayores que a y menores que b.
(a,
b) = {x 
 / a < x < b}
/ a < x < b}
Intervalo cerrado
Intervalo
cerrado, [a, b],
es el conjunto de todos los números reales mayores o iguales que a y menores
o iguales que b.
[a,
b] = {x 
 / a ≤ x ≤ b}
/ a ≤ x ≤ b}
Intervalo semiabierto por la izquierda
Intervalo
semiabierto por la izquierda,
(a, b], es el conjunto de todos los números reales mayores que a y
menores o iguales que b.
(a,
b] = {x 
 / a < x ≤ b}
/ a < x ≤ b}
Intervalo semiabierto por la derecha
Intervalo
semiabierto por la derecha,
[a, b), es el conjunto de todos los números reales mayores o iguales
que a y menores que b.
[a,
b) = {x 
 / a ≤ x < b}
/ a ≤ x < b}
ejercicios:
Expresa en lenguaje matemático los siguientes intervalos:

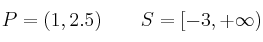

![Q=[-2,3] \qquad T=(2, +\infty) Q=[-2,3] \qquad T=(2, +\infty)](http://matematicasies.com/local/cache-TeX/f00c8e4b00cd34418276d7a56a52f38b.png)

![R=[-7,0] \qquad I=(-5, 2] R=[-7,0] \qquad I=(-5, 2]](http://matematicasies.com/local/cache-TeX/b088ec574587b57d7f8d50c5ade01859.png)
Representa gráficamente y expresa simbólicamente las siguientes expresiones:

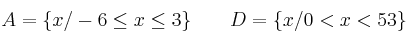

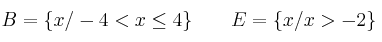

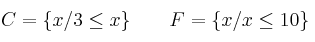
No hay comentarios:
Publicar un comentario